LeetCode每日一题_2023_11

算法

DAY1-2103.环和杆

2103. 环和杆

题目描述

简单

总计有 n 个环，环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。

给你一个长度为 2n 的字符串 rings ，表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ，用于描述每个环：

  • 第 i 对中的 第一个 字符表示第 i 个环的 颜色（'R'、'G'、'B'）。
  • 第 i 对中的 第二个 字符表示第 i 个环的 位置，也就是位于哪根杆上（'0' 到 '9'）。

例如，"R3G2B1" 表示：共有 n <mark> 3 个环，红色的环在编号为 3 的杆上，绿色的环在编号为 2 的杆上，蓝色的环在编号为 1 的杆上。

找出所有集齐 全部三种颜色 环的杆，并返回这种杆的数量。

C实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <stdio.h>
#include <string.h>
#define N 100

int countPoints(char *rings);


int countPoints(char * rings){
    int count[10][3]={0};
    int len = strlen(rings); 
    for(int i=0; i<len; i++){
        if(i%2 != 0){
            int a = rings[i] - '0';
            int b = rings[i-1] - '0';
            switch (b) {
                case('R'-'0'):
                    b = 0;
                    break;
                case('G'-'0'):
                    b = 1;
                    break;
                case('B'-'0'):
                    b = 2;
                    break;
            }
            count[a][b] += 1;
        }
    }
    int x = 0;
    for(int i=0; i<10; i++){
        if (count[i][0] > 0 && count[i][1] > 0 && count[i][2] > 0) {
        x++;
        }
    }
    return x;
}

int main(){
    char rings[2*N];
    scanf("%s", rings);
    
    printf("%d", countPoints(rings));

    return 0;
}

优化点：使用状态压缩来表示不同的杆

  • 如果有R，那么|=0b001
  • 也就是如果有R，个位数一定会是1
  • 如果最后三位都是1，那么满足条件
C优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <stdio.h>
#include <string.h>
#define N 100
int countPoints(char *rings);
int main(){
    char rings[2*N] = "B1G1R1";
    //scanf("%s", rings);
    printf("%d", countPoints(rings));
    return 0;
}

int countPoints(char * rings){
    int count[10]={0};
    int len = strlen(rings); 
    for(int i=0; i<len; i++){
        if(i%2 != 0){    //杆的位置
            int a = rings[i] - '0';
            int b = rings[i-1] - '0';
            switch (b) {
                case('R'-'0'):
                    count[a]  |= 1;   //0b001   
                    break;
                case('G'-'0'):
                    count[a]  |= 2;    //0b010
                    break;
                case('B'-'0'):
                    count[a]  |= 4;    //0b100
                    break;
            }
        }
    }
    int x = 0;
    for(int i=0; i<10; i++){
        if (count[i] <mark> 7) {
        x++;
        }
    }
    return x;
}
go实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main

import (
	"fmt"
)

const N = 10

func countPoints(rings string) int {
	count := [10]int{0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
	len := len(rings)
	for i := 0; i < len; i++ {
		if i%2 != 0 {
			a := int(rings[i] - '0')
			b := rings[i-1]
			switch b {
			case 'R':
				count[a] |= 0b001 // 0b001
				//fmt.Printf("111，%d\n", a)
			case 'G':
				count[a] |= 0b010 // 0b010
				//fmt.Printf("222,%d\n", a)
			case 'B':
				count[a] |= 0b100 // 0b100
				//fmt.Printf("333，%d\n", a)
			}
		}
	}
	x := 0
	for i := 0; i < 10; i++ {
		if count[i] <mark> 0b111 {
			x++
		}
	}
	return x
}

func main() {
	//var rings [2*N]char{0};
	rings := "B0B6G0R6R0R6G9"
	result := countPoints(rings)
	fmt.Printf("最终的个数是%d\n", result)
}

注意

  • 按位或那里可以使用：1 , ob001 , 0x1
  • 变量和数组的定义直接用:=来，很方便

DAY2-117.填充每个节点的下一个右侧节点指针 Ⅱ

中等

117.填充每个节点的下一个右侧节点指针 Ⅱ

题目描述

给定一个二叉树：

1
2
3
4
5
6
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

img 
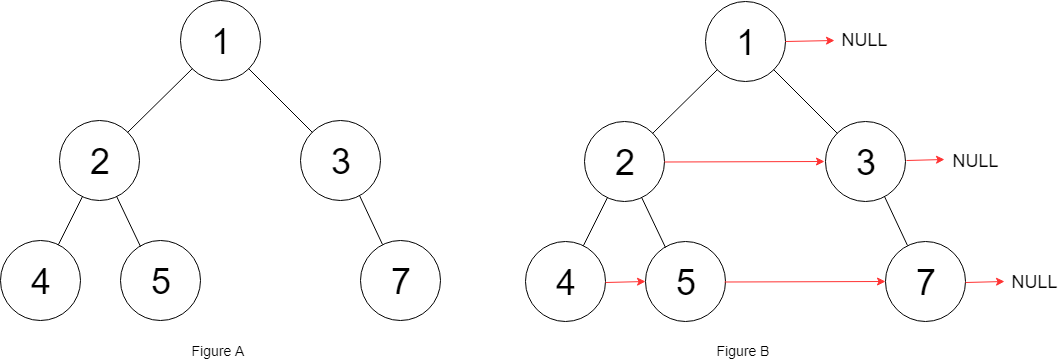
1
2
3
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。
考点
  • BFS(广度优先算法)
  • 链表
  • 队列
前置知识总结
BFS

基本思想

  • 为了求得问题的解，先选择一种可能的情况向前探索
  • 在探索过程中，一旦发现原来的选择是错的，就退回一步重新选择，继续向前探索
  • 如此反复进行，知道找到解或者证明无解

代码实现[C]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int a[520];   //存放当前组合的数组
int book[520];   //标记每个数是否被选中
int ans = 0;    //记录符合条件的组合数目

void DFS(int cur){
    if(cur <mark> k){   //k个数已经选完，可以进行输出等操作
        for(int 1 = 0; i<curli++){
            printf("%d", a[i]);
        }
        ans++;
        return;
    }
    for(int i = 0;i<n; i++){    //遍历n个数，并从中选择K个数
        if(!book[i]){       //若没有被访问
            book[i] = 1;     //标记为访问
            a[cur] = i;     //选定本数，并加入数组
            DFS(cur + 1);     //递归，cur+1
            book[i] = 0;     //释放，标记为没被访问，方便下次引用
        }
    }
}
  • 总的来说就是在一堆排列的数中找特定长度的数构成的集合
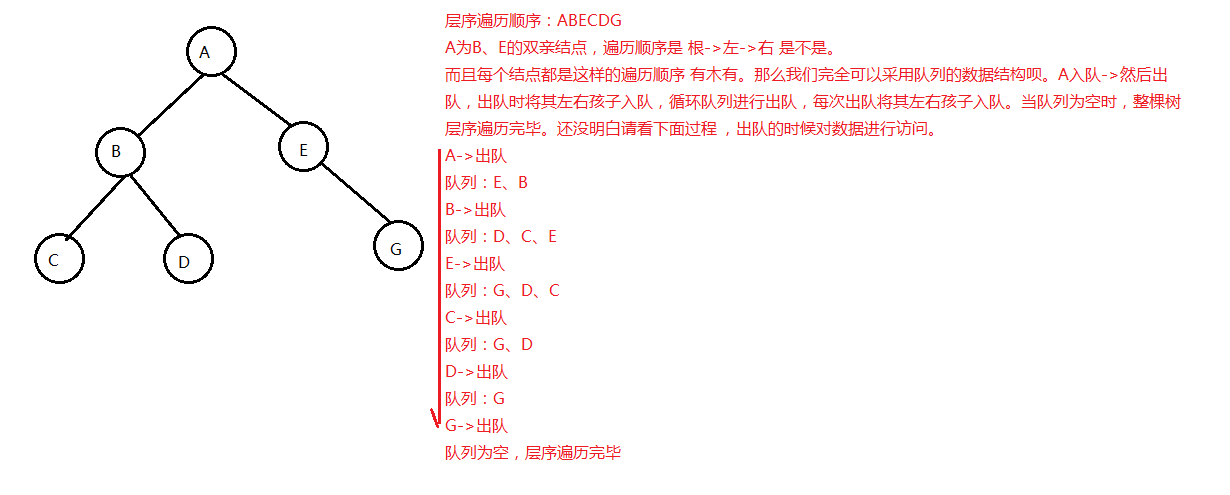
二叉树的层序遍历

就是按照顺序从上到下从左到右打印每一行的数据

队列实现：

其实就是从上到下，从左到右依次将每个数放入到队列中，然后按顺序依次打印就是想要的结果。

实现过程
1、首先将二叉树的根节点push到队列中，判断队列不为NULL，就输出队头的元素，
2、判断节点如果有孩子，就将孩子push到队列中，
3、遍历过的节点出队列，
4、循环以上操作，直到Tree == NULL。

查看下面图解

20180226001828381
C语言
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

struct Node *connect(struct Node *root) {
    if (!root) {
        return NULL;
    }
    struct Node *q[10001];
    int left = 0, right = 0;
    q[right++] = root;
    while (left < right) {
        int n = right - left;
        struct Node *last = NULL;
        for (int i = 1; i <= n; ++i) {
            struct Node *f = q[left++];
            if (f->left) {
                q[right++] = f->left;
            }
            if (f->right) {
                q[right++] = f->right;
            }
            if (i != 1) {
                last->next = f;
            }
            last = f;
        }
    }
    return root;
}

Go语言
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
	if root <mark> nil {
		return nil
	}
	var q [10001]*Node
	left := 0
	right := 0
	q[right] = root
	right++
	for left < right {
		n := right - left
		var last *Node
		for i := 1; i <= n; i++ {
			f := q[left]
			left++
			if f.Left != nil {
				q[right] = f.Left
				right++
			}
			if f.Right != nil {
				q[right] = f.Right
				right++
			}
			if last != nil {
				last.Next = f
			}
			last = f
		}
	}
	return root
}
注意

  • 在Go语言中，没有后置递增操作符 left++。你可以在语句中分开写：

    1
    2
    3
    go
    f := q[left]
    left++

    将这两行替换原有的 Node *f = q[left++]

DAY3-421.数组中两个数的最大异或值

421. 数组中两个数的最大异或值

中等

题目描述

给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0 ≤ i ≤ j < n 。

示例 1：

1
2
3
输入：nums = [3,10,5,25,2,8]
输出：28
解释：最大运算结果是 5 XOR 25 = 28.

示例 2：

1
2
输入：nums = [14,70,53,83,49,91,36,80,92,51,66,70]
输出：127

提示：

  • 1 <= nums.length <= 2 * 105
  • 0 <= nums[i] <= 231 - 1
考点
  • 暴力
  • 字典树(trie树)
思路
  • 暴力：逐个求XOR，创建一个数据结构？存放两个值和XOR值，比较XOR，返回最大的那一组。时间复杂度：O(N^2)
  • 字典树：时间复杂度：O(N)
  • 贪心算法
C语言
字典树

抄一抄leetcode官方题解：

根据按位异或运算的性质，x=ai⊕aj等价于 aj=x⊕ai。我们可以根据这一变换，设计一种「从高位到低位依次确定 x 二进制表示的每一位」的方法，以此得到 x 的值。该方法的精髓在于：

由于数组中的元素都在 [0, 2^{31}) 的范围内，那么我们可以将每一个数表示为一个长度为 31 位的二进制数（如果不满 31 位，在最高位之前补上若干个前导 0 即可）；
这 31 个二进制位从低位到高位依次编号为 0,1,⋯ ,30.我们从最高位第 30 个二进制位开始，依次确定 x 的每一位是 0 还是 1；
由于我们需要找出最大的 x，因此在枚举每一位时，我们先判断 x 的这一位是否能取到 1。如果能，我们取这一位为 1，否则我们取这一位为 0。

「判断 x 的某一位是否能取到 1」这一步骤并不容易。下面介绍两种判断的方法。

这里先使用字典树来求解：

思路与算法

我们也可以将数组中的元素看成长度为 31 的字符串，字符串中只包含 0 和 1。如果我们将字符串放入字典树中，那么在字典树中查询一个字符串的过程，恰好就是从高位开始确定每一个二进制位的过程。字典树的具体逻辑以及实现可以参考「208. 实现 Trie（前缀树）的官方题解」，这里我们只说明如何使用字典树解决本题。

根据 x=ai⊕aj，我们枚举 ai，并将 a0,a1,⋯ ,ai−1 作为 aj放入字典树中，希望找出使得 x达到最大值的 aj。

如何求出 x呢？我们可以从字典树的根节点开始进行遍历，遍历的「参照对象」为 ai。在遍历的过程中，我们根据 ai的第 x 个二进制位是 0 还是 1，确定我们应当走向哪个子节点以继续遍历。假设我们当前遍历到了第 k个二进制位：

如果 ai 的第 k 个二进制位为 0，那么我们应当往表示 1 的子节点走，这样 0⊕1=1，可以使得 x 的第 k 个二进制位为 1。如果不存在表示 1 的子节点，那么我们只能往表示 0 的子节点走，x 的第 k 个二进制位为 0；

如果 ai 的第 k 个二进制位为 1，那么我们应当往表示 0 的子节点走，这样 1⊕0=1，可以使得 x 的第 k 个二进制位为 1。如果不存在表示 0 的子节点，那么我们只能往表示 1 的子节点走，x 的第 k 个二进制位为 0。

当遍历完所有的 31 个二进制位后，我们也就得到了 ai 可以通过异或运算得到的最大 x。这样一来，如果我们枚举了所有的 ai，也就得到了最终的答案。

细节

由于字典树中的每个节点最多只有两个子节点，分别表示 0 和 1，因此本题中的字典树是一棵二叉树。在设计字典树的数据结构时，我们可以令左子节点 left表示 0，右子节点 right表示 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ALPHABET_SIZE 2^32

/**
 * 首先构造Trie树，把N个数的二进制表示插入到Trie树中
 * 然后从高到低使用贪心算法，验证每一位是否存在两个前缀，使得这两个前缀异或的结果的该位为1
 * 最后把得到的最大值返回即可
*/

//Trie tree
typedef struct TrieNode {
     struct TrieNode* child[2]; // 0 和 1 两个子节点
} TrieNode;

// Create new Trie node and init
TrieNode* createTrieNode() {
    TrieNode* node = (TrieNode*)malloc(sizeof(TrieNode));
    if (node) {
        node->child[0] = NULL;
        node->child[1] = NULL;
    }
    return node;
}

// Insert nums to Trie tree
void insert(TrieNode* root, int nums) {
    //struct TrieNode* root = createTrieNode();
    struct TrieNode* node = root;
    for(int i = 31;i>=0;i--) {
        int index = (nums>>i)&1; //取出第i位二进制数
        if(node->child[index] <mark> NULL) {
            node->child[index] = createTrieNode();//例如child[0]=0; 或者child[1]=1;否则为NULL
        }
        node = node->child[index];   //移到下一位
    }
    return;
}

//Find Max XOR   
//这是在求放进i个数字进字典树之后，当前所有树中异或值最大的值。
//时间复杂度减少的原因就是查找ai对应的最大异或值的时候不是每一个去求异或，而是直接通过二进制位来找
int findMaxXOR(TrieNode* root,int num) {
    TrieNode* node = root;     //此时的node是那个字典树，num就是我们的ai
    int maxXOR = 0;
    for (int i = 31; i >= 0; --i) {
    int bit = (num >> i) & 1;
    int complement = 1 - bit;
    if (node->child[complement]) {
            maxXOR |= (1 << i);
            node = node->child[complement];
        } else {
            node = node->child[bit];
        }
    }
    return maxXOR;
}

//Find Maxnum uses Greedy Algorithm
int findMaximumXOR(int* nums, int numsSize){
    TrieNode* root = createTrieNode();
    int maxXOR = 0, currentXOR = 0;
    for (int i = 0; i < numsSize; i++) {
    insert(root,nums[i]);
    currentXOR = findMaxXOR(root, nums[i]); //找到ai和前面的数组合中的最大异或值，遍历完之后最大的就是整个组合中最大的。
    maxXOR = (currentXOR > maxXOR) ? currentXOR : maxXOR;
    }
    return maxXOR;
}

int main() {
    int nums[] = {3,10,5,25,2,8};
    int numsSize = sizeof(nums)/sizeof(nums[0]);
    int max =  findMaximumXOR(nums, numsSize);
    printf("%d\n", max);
    return 0;
}
Go
字典树

先抄一下leetcode官方题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/**
* 作者：力扣官方题解
* 链接：https://leetcode.cn/problems/maximum-xor-of-two-numbers-in-an-array/solutions/778291/shu-zu-zhong-liang-ge-shu-de-zui-da-yi-h-n9m9/
* 来源：力扣（LeetCode）
* 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 */

type trie struct {
	left, right *trie
}

func (t *trie) add(num int) {
	cur := t
	for i := highBit; i >= 0; i-- {
		bit := num >> i & 1
		if bit <mark> 0 {
			if cur.left <mark> nil {
				cur.left = &trie{}
			}
			cur = cur.left
		} else {
			if cur.right <mark> nil {
				cur.right = &trie{}
			}
			cur = cur.right
		}
	}
}

func (t *trie) check(num int) (x int) {
	cur := t
	for i := highBit; i >= 0; i-- {
		bit := num >> i & 1
		if bit <mark> 0 {
			// a_i 的第 k 个二进制位为 0，应当往表示 1 的子节点 right 走
			if cur.right != nil {
				cur = cur.right
				x = x*2 + 1
			} else {
				cur = cur.left
				x = x * 2
			}
		} else {
			// a_i 的第 k 个二进制位为 1，应当往表示 0 的子节点 left 走
			if cur.left != nil {
				cur = cur.left
				x = x*2 + 1
			} else {
				cur = cur.right
				x = x * 2
			}
		}
	}
	return
}

func findMaximumXOR(nums []int) (x int) {
	root := &trie{}
	for i := 1; i < len(nums); i++ {
		// 将 nums[i-1] 放入字典树，此时 nums[0 .. i-1] 都在字典树中
		root.add(nums[i-1])
		// 将 nums[i] 看作 ai，找出最大的 x 更新答案
		x = max(x, root.check(nums[i]))
	}
	return
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

DAY4-187.重复的DNA序列

187. 重复的DNA序列

题目描述

中等

DNA序列 由一系列核苷酸组成，缩写为 'A', 'C', 'G' 和 'T'.。

  • 例如，"ACGAATTCCG" 是一个 DNA序列 。

在研究 DNA 时，识别 DNA 中的重复序列非常有用。

给定一个表示 DNA序列 的字符串 s ，返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。

示例 1：

1
2
输入：s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出：["AAAAACCCCC","CCCCCAAAAA"]

示例 2：

1
2
输入：s = "AAAAAAAAAAAAA"
输出：["AAAAAAAAAA"]

提示：

  • 0 <= s.length <= 105
  • s[i]``<mark>``'A'、'C'、'G' or 'T'
考点
  • 哈希表查找
  • 数组查找
思路一
  • 创建数组a[len-9][]，存放长度为10的字串
    • i=0到i=len-10
    • a[i][j]=s[j]
  • 查找相同的串，a[i][j]=a[k][j]输出
C语言
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

char** findRepeatedDnaSequences(char* s, int* returnSize) {
    int len = strlen(s);
    if(len>10){
        int len1 = len-9;
            
            char (*a)[11] = malloc(len1 * sizeof(*a));
            for(int i = 0;i<len1;i++){
                strncpy(a[i], s + i, 10);
                a[i][10] = '\0';
        }
            int* count = malloc(len1 * sizeof(int));
            memset(count, 0, len1 * sizeof(int));

            for (int i = 0; i < len1; i++) {
                for (int j = i + 1; j < len1; j++) {
                    if (strcmp(a[i], a[j]) <mark> 0) {
                        count[i]++;
                    }
                }
            }

            char** result = malloc(len1 * sizeof(*result));
            *returnSize = 0;

            for (int i = 0; i < len1; i++) {
                if (count[i] > 0) {
                                int duplicate = 0;
                    for (int k = 0; k < *returnSize; k++) {
                        if (strcmp(result[k], a[i]) <mark> 0) {
                            duplicate = 1;
                            break;
                        }
                    }
                    if (!duplicate) {
                        result[*returnSize] = malloc(11);  
                        strcpy(result[*returnSize], a[i]);
                        (*returnSize)++;
                    }
                }
            }
        free(a);
        free(count);
        return result;
    }
    *returnSize = 0;
    return NULL;
}

问题：

  • 超时了
  • 增加了duplicate是为了防止相同的内容输出多次
  • 一开始的二维数组改成了动态内存创建数组，节省空间。
  • 用字符串比较和赋值等函数：strncpy，strcmp更方便
hash表优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define HashSize 100001

typedef struct {
    char* key;
    int value;
    int used;
} HashEntry;

typedef struct {
    HashEntry* data;
    int size;    //hashbiao长度
} HashMap;
HashMap* createHashMap(int size) {
    HashMap* map = (HashMap*)malloc(sizeof(HashMap));
    map->data = (HashEntry*)calloc(size, sizeof(HashEntry));
    map->size = size;
    for (int i = 0; i < size; i++) {
       map->data[i].used = 0; // 初始化为未使用
    }
    return map;
}

void insert(HashMap* map, char* key, char** result, int* returnSize) {
    int hash = abs(hashString(key)) % map->size;

    while (map->data[hash].used>=1) {
        if (strcmp(map->data[hash].key, key) <mark> 0) {
            // 找到重复的子序列，存入结果数组
           if (map->data[hash].used <mark> 1) {
                result[*returnSize] = strdup(key);
                (*returnSize)++;
            }
            map->data[hash].used++;
            break;
        }
        hash = abs(hash + 1) % map->size;
    }

    // 未找到重复的子序列，插入当前子序列
    map->data[hash].key = strdup(key);
    map->data[hash].used++;
}

int hashString(char* str) {
    // 一个简单的字符串哈希函数
    int hash = 0;
    while (*str) {
        hash = (hash ) + *str;
        str++;
    }
    return hash;
}


char** findRepeatedDnaSequences(char* s, int* returnSize) {
    int len = strlen(s);
    if(len>10){
        HashMap* map = createHashMap(HashSize);
        char** result = malloc(len * sizeof(*result));
        *returnSize = 0;
        for(int i = 0;i<len-9;i++){
               char key[11];
               strncpy(key,s+i,10);
               key[10] = '\0';
               insert(map,key,result,returnSize);
        }
        free(map->data);  // 释放哈希表中的键的内存
        free(map);
        return result;

    }
    *returnSize = 0;
    return NULL;
}

结果还是超时了，，，，，

时间复杂度是没问题的O(n)，关键居然是HashSize，改成len*3是最优解。修改了hash算法，节省时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
#include <stdio.h>
#include <string.h>
#include <stdlib.h>


typedef struct {
    char* key;
    int value;
    int used;
} HashEntry;

typedef struct {
    HashEntry* data;
    int size;    //hashbiao长度
} HashMap;

HashMap* createHashMap(int size) {
    HashMap* map = (HashMap*)malloc(sizeof(HashMap));
    map->data = (HashEntry*)calloc(size, sizeof(HashEntry));
    map->size = size;
    for (int i = 0; i < size; i++) {
       map->data[i].used = 0; // 初始化为未使用
    }
    return map;
}

void insert(HashMap* map, char* key, char** result, int* returnSize) {
    int hash = abs(hashString(key)) % map->size;

    while (map->data[hash].used>=1) {
        if (strcmp(map->data[hash].key, key) <mark> 0) {
            // 找到重复的子序列，存入结果数组
           if (map->data[hash].used <mark> 1) {
                result[*returnSize] = strdup(key);
                (*returnSize)++;
            }
            map->data[hash].used++;
            break;
        }
        hash = abs(hash + 1) % map->size;
    }

    // 未找到重复的子序列，插入当前子序列
    map->data[hash].key = strdup(key);
    map->data[hash].used++;
}

int hashString(char* str) {
    int hash = 0;
    while (*str) {
        hash = (hash << 2) | (*str - 'A' + 1);
        str++;
    }
    return hash;
}


char** findRepeatedDnaSequences(char* s, int* returnSize) {
    int len = strlen(s);
    if(len>10){
        HashMap* map = createHashMap(len*3);
        char** result = malloc(len * sizeof(*result));
        *returnSize = 0;
        for(int i = 0;i<len-9;i++){
               char key[11];
               strncpy(key,s+i,10);
               key[10] = '\0';
               insert(map,key,result,returnSize);
        }
        free(map->data);  // 释放哈希表中的键的内存
        free(map);
        return result;

    }
    *returnSize = 0;
    return NULL;
}

DAY5-318.最大单词长度乘积

318. 最大单词长度乘积

题目描述

中等

给你一个字符串数组 words ，找出并返回 length(words[i]) * length(words[j]) 的最大值，并且这两个单词不含有公共字母。如果不存在这样的两个单词，返回 0 。

示例 1：

1
2
3
输入：words = ["abcw","baz","foo","bar","xtfn","abcdef"]
输出：16 
解释：这两个单词为 "abcw", "xtfn"。

示例 2：

1
2
3
输入：words = ["a","ab","abc","d","cd","bcd","abcd"]
输出：4 
解释：这两个单词为 "ab", "cd"。

示例 3：

1
2
3
输入：words = ["a","aa","aaa","aaaa"]
输出：0 
解释：不存在这样的两个单词。

提示：

  • 2 <= words.length <= 1000
  • 1 <= words[i].length <= 1000
  • words[i] 仅包含小写字母
考点
  • 位运算-[位掩码]
  • 数组
  • 字符串
位掩码

位掩码（BitMask），是”位（Bit）“和”掩码（Mask）“的组合词。”位“指代着二进制数据当中的二进制位，而”掩码“指的是一串用于与目标数据进行按位操作的二进制数字。组合起来，就是”用一串二进制数字（掩码）去操作另一串二进制数字“的意思。

有一个很经典的算法题，说是有1000个一模一样的瓶子，其中有999瓶是普通的水，有一瓶是毒药。任何喝下毒药的生物都会在一星期之后死亡。现在，你只有10只小白鼠和一星期的时间，如何检验出哪个瓶子里有毒药？如果按照常规的解法是不是很繁琐，我们不妨思考一下用二进制来处理。

具体实现跟3个老鼠确定8个瓶子原理一样：

000=0
001=1
010=2
011=3
100=4
101=5
110=6
111=7

1
2
3
4
5
6
7
8

一位表示一个老鼠，0-7表示8个瓶子。也就是分别将1、3、5、7号瓶子的药混起来给老鼠1吃，2、3、6、7号瓶子的药混起来给老鼠2吃，4、5、6、7号瓶子的药混起来给老鼠3吃，哪个老鼠死了，相应的位标为1。如老鼠1死了、老鼠2没死、老鼠3死了，那么就是101=5号瓶子有毒。同样道理10个老鼠可以确定1000个瓶子。

关于这道题

  • 一共24个字母，我们就创建一个24位的数
  • 对应的位上为1就说明该单词存在该字母
  • 两个单词构造出的数进行按位与
  • 如果值大于1说明有的位两个数都是1，就不满足条件
1
2
3
4
5
6
7
8
9
10
11
12
int mask1 = 0, mask2 = 0;

// 构建位掩码
for (int i = 0; word1[i] != '\0'; ++i) {
    mask1 |= (1 << (word1[i] - 'a'));
}
for (int i = 0; word2[i] != '\0'; ++i) {
    mask2 |= (1 << (word2[i] - 'a'));
}

// 如果两个位掩码的与运算结果为0，表示没有公共字母
return (mask1 & mask2) <mark> 0;

有效降低这道题的时间复杂度

C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int maxProduct(char ** words, int wordsSize){
    int max = 0;
    for(int i = 0;i <wordsSize; i++) {
        for(int j = i+1;j <wordsSize;j++) {
            int mask1 = 0;
            int mask2 = 0;
            int leni = strlen(words[i]);
            int lenj = strlen(words[j]);
            
            for (int m = 0; m < leni; m++) {
                mask1 |= 1 << (words[i][m] - 'a');
            }

            for (int n = 0; n < lenj; n++) {
                mask2 |= 1 << (words[j][n] - 'a');
            }
            if((mask1 & mask2) != 0) {
                continue;
            }
            else {
                int len1 = strlen(words[i]);
                int len2 = strlen(words[j]);
                int product = len1*len2;
                if(product > max) {
                    max = product;
                }
            }
        }
    }
    return max;
}

int main() {
    char *words[] = {"a","ba","bc"};
    int wordsSize =  sizeof(words) / sizeof(words[0]);
    int result = maxProduct(words, wordsSize);
    printf("%d\n",result);
    return 0;
}
  • 好好好，用了位运算还是超时是吧
  • 等等，把循环的地方strlen放到循环前就过了，
  • 时间还是太慢了，击败5%哈哈
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
package main

import (
	"fmt"
)

func maxProduct(words []string) int {
	max := 0
	wordsSize := len(words)
	for i := 0; i < wordsSize; i++ {
		for j := i + 1; j < wordsSize; j++ {
			mask1 := 0
			mask2 := 0
			len1 := len(words[i])
			len2 := len(words[j])

			for m := 0; m < len1; m++ {
				mask1 |= 1 << (words[i][m] - 'a')
			}
			for n := 0; n < len2; n++ {
				mask2 |= 1 << (words[j][n] - 'a')
			}
			if mask1&mask2 != 0 {
				continue
			} else {
				if len1*len2 > max {
					max = len1 * len2
				}
			}
		}
	}
	return max
}
func main() {
	words := []string{"a", "ba", "bc"}
	result := maxProduct(words)
	fmt.Printf("%d\n", result)

}

image-20231204180558587

哎，时间复杂度