AC自动机

算法

AC自动机

AC自动机是最一种多模式匹配算法，它由贝尔实验室的两位研究人员Alfred V. Aho 和 Margaret J.Corasick 于1975年发明，几乎与KMP算法同时问世，至今仍然在模式匹配领域被广泛应用。例如：在一篇文章中，需要找到多个词汇所在的位置和出现频率。

其核心算法仍是寻找模式串内部规律，进行每次失配的高效跳转。这点和KMP算法一致，不同点在于,AC自动机寻找模式串的相同前缀。

在这之前，先了解一下KMP算法和Trie数。

KMP算法

Brute-Force算法

首先介绍字符串匹配问题——经典的Brute-Force算法

就是按照顺序移动字串，让其和主串做比较。当发现字串和主串对应相等后，就返回匹配到的主串的第一个字符的位置，C语言实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <string.h>

int Brute_Forece(const char *text,const char *pattren){
    int textLentg = strlen(text);
    int patternLength = (strlen(pattern));
    
    for( int i = 0;i <= textLength - patternLength;i++){
        for(int j = 0;j < patternLength;j++){
            if(text[i+j] != pattern[j]){
                break;
            }
        }
        if(j == patternLength){
            return i;
        }
    }
    return -1;
}


时间复杂度O(mn)

KMP算法

原理就是在进行一次匹配之后就初步哦按段后续几趟匹配一定不会成功，然后跳过，具体做法是为主串中每一个字符添加一个Next值。

next数组的定义为：next[i]表示模式串A[0]至A[i]这个字串，使得前k个字符等于后k个字符的最大值，特别的k不能取i+i,因为字串一共才i+1个字符，自己跟自己相等毫无意义。

如何通过next数组来确定到底要跳多少步？ 

1
2
3
4
主串:			[A,B,A,B,A,A,B,A,A,B,A,C]
			  |
子串:         [A,B,A,A,B,A,C]
next数组:		[0,0,1,1,2,3,0]
  • 当字串和主串第一个匹配之后，成功匹配上3个字符
  • 表示总共重复了next[3-1]=next[2]=1个，于是直接跳过：匹配上的次数-重复的个数=3-1=2步
1
2
3
4
主串:			[A,B,A,B,A,A,B,A,A,B,A,C]
			      |
子串:             [A,B,A,A,B,A,C]
next数组:		    [0,0,1,1,2,3,0]
  • 这一次匹配了6个，就是next[6-1]=next[5]=3
  • 表示重复了3个，直接跳过6-3=3步。
1
2
3
4
主串:			[A,B,A,B,A,A,B,A,A,B,A,C]
			            |
子串:                   [A,B,A,A,B,A,C]
next数组:		          [0,0,1,1,2,3,0]
  • 匹配成功

所以关键就是建立next数组

Next数组

暴力构建法，时间复杂度为O(m^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void buildNextArr(const char *pattern, int *next) {
    int m = strlen(pattern);

    for (int i = 0; i < m; i++) {
        int len = 0;
        for (int j = 0; j < i; j++) {
            int k = 0;
            while (k < j && pattern[k] == pattern[i - j + k]) {
                k++;
            }
            if (k == j) {
                len = j + 1;
            }
        }
        next[i] = len;
    }
}

递推法构建，时间复杂度为O(n+m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void buildNextRecursive(const char *pattern, int *next, int i, int j, int len) {
    if (i == len) {
        return;
    }

    if (j == -1 || pattern[i] == pattern[j]) {
        next[i + 1] = j + 1;
        buildNextRecursive(pattern, next, i + 1, j + 1, len);
    } else {
        buildNextRecursive(pattern, next, i, next[j], len);
    }
}

void buildNextArr(const char *pattern, int *next) {
    int m = strlen(pattern);
    next[0] = -1;
    buildNextRecursive(pattern, next, 0, -1, m);
}
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <string.h>

void buildNextRecursive(const char *pattern, int *next, int i, int j, int len) {
    if (i == len) {
        return;
    }

    if (j == -1 || pattern[i] == pattern[j]) {
        next[i + 1] = j + 1;
        buildNextRecursive(pattern, next, i + 1, j + 1, len);
    } else {
        buildNextRecursive(pattern, next, i, next[j], len);
    }
}

void buildNext(const char *pattern, int *next) {
    int m = strlen(pattern);
    next[0] = -1;
    buildNextRecursive(pattern, next, 0, -1, m);
}

int kmpSearch(const char *text, const char *pattern) {
    int n = strlen(text);
    int m = strlen(pattern);

    int next[m];
    buildNext(pattern, next);

    int i = 0, j = 0;
    while (i < n && j < m) {
        if (j == -1 || text[i] == pattern[j]) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }

    if (j == m) {
        return i - m; // 匹配成功，返回匹配的起始位置
    } else {
        return -1; // 未找到匹配
    }
}

int main() {
    const char *text = "ababcababcabcabc";
    const char *pattern = "abcabc";

    int result = kmpSearch(text, pattern);

    if (result != -1) {
        printf("Pattern found at position: %d\n", result);
    } else {
        printf("Pattern not found.\n");
    }

    return 0;
}

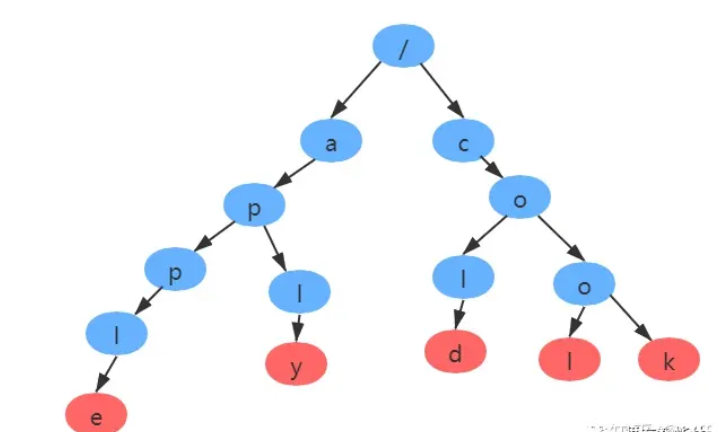
Trie树

Tire树也叫字典树，是一种特殊的前缀树结构。它是哈希树的一种变种，专门为字符串处理设计的数据结构。典型的应用是用于统计和排序大量的字符串（不限于字符串）因此经常被搜索引擎用于文字词频统计。它的优点是：最大限度地减少无谓的字符串比较。Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

如图：

image-20231118100217713

前缀树的3个基本性质：

  • 根节点不包含字符，除根节点外每一个节点只包含一个字符。
  • 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
  • 每个节点的所有子节点包含的字符都不相同。

应用

  • **字符串检索:**事先将已知的一些字符串（字典）的有关信息保存到trie树里，查找另外一些未知字符串是否出现过或者出现频率。
  • 字符串最长公共前缀:Trie树利用多个字符串的公共前缀来节省存储空间，反之，当我们把大量字符串存储到一棵trie树上时，我们可以快速得到某些字符串的公共前缀。
  • 排序:Trie树是一棵多叉树，只要先遍历整棵树，输出相应的字符串便是按字典序排序的结果。

C语言实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <stdio.h>
#include <stdlib.h>

#define ALPHABET_SIZE 26    //这里只考虑了26个英文小写字母。如果考虑中文就是加上特殊编，增加ALPHABET_SIZE

// Trie 树节点结构
struct TrieNode {
    struct TrieNode* children[ALPHABET_SIZE];    
    int isEndOfWord;
};

// 创建新的 Trie 节点，初始化
struct TrieNode* createTrieNode() {
    struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
    if (node) {
        for (int i = 0; i < ALPHABET_SIZE; i++) {
            node->children[i] = NULL;
        }
        node->isEndOfWord = 0;
    }
    return node;
}

// 插入字符串到 Trie 树
void insert(struct TrieNode* root, const char* key) {
    struct TrieNode* node = root;
    for (int i = 0; key[i] != '\0'; i++) {
        int index = key[i] - 'a';
        if (node->children[index] == NULL) {
            node->children[index] = createTrieNode();
        }
        node = node->children[index];
    }
    node->isEndOfWord = 1;
}

// 搜索字符串在 Trie 树中是否存在
int search(struct TrieNode* root, const char* key) {
    struct TrieNode* node = root;
    for (int i = 0; key[i] != '\0'; i++) {
        int index = key[i] - 'a';
        if (node->children[index] == NULL) {
            return 0; // 未找到字符串
        }
        node = node->children[index];
    }
    return (node != NULL && node->isEndOfWord);
}

// 释放 Trie 树的内存
void freeTrie(struct TrieNode* root) {
    if (root == NULL) {
        return;
    }
    for (int i = 0; i < ALPHABET_SIZE; i++) {
        freeTrie(root->children[i]);
    }
    free(root);
}

int main() {
    struct TrieNode* root = createTrieNode();

    // 插入一些字符串
    insert(root, "apple");
    insert(root, "app");

    // 搜索字符串
    printf("%s\n", search(root, "apple") ? "Found" : "Not found");
    printf("%s\n", search(root, "apples") ? "Found" : "Not found");

    // 释放 Trie 树的内存
    freeTrie(root);

    return 0;
}

AC自动机

核心算法仍是寻找模式串内部规律，进行每次失配的高效跳转。这点和KMP算法一致，不同点在于,AC自动机寻找模式串的相同前缀。

AC自动机使用前缀树来存放所有模式串的前缀，通过失配指针来处理失配的跳转。AC自动机的构建，首先需要构建Trie树，其次需要添加失配指针（fail表），最后需要模式匹配。

核心思想就是trie树的匹配模式，加上类似于KMP中next数组的fail表，来进行每次失配的高效跳转

  • 构建Trie树

之前已经讲过，不再赘述

  • 构建fail表

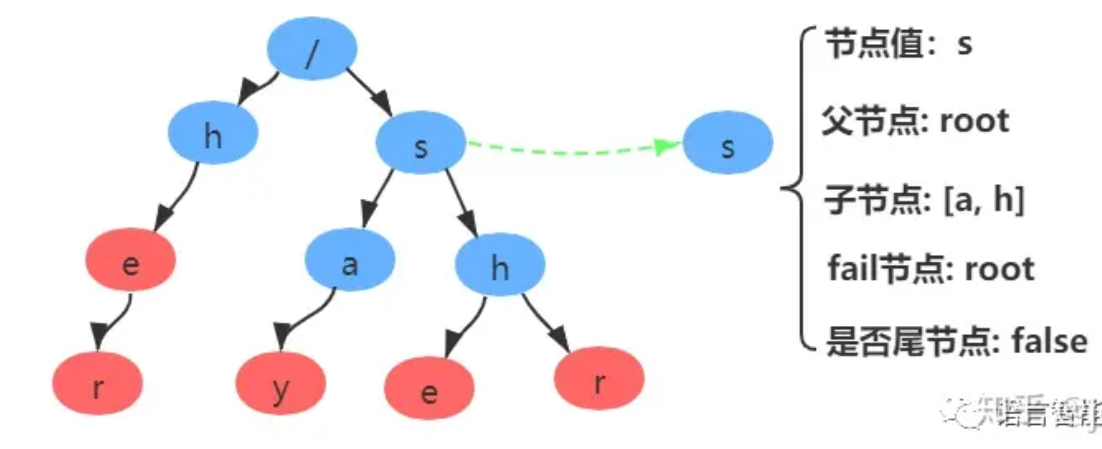
构建fail表之前，我们需要明确，每个节点：父节点、子节点列表、fail节点、节点的值和是否是尾节点这几个属性组成：

image-20231118102636608

fail表中保存了失配时的fail指针，fail指针就是当前位置失配以后能够跳转继续进行匹配的字符位置，达到匹配过程中不需要回溯的效果。构建过程使用了BFS（宽度优先搜索）算法。搜索过程文字描述：

假设当前节点为temp, 我们找到temp的父节点，得到父节点的fail节点，再找到fail节点的所有子节点，寻找子节点中是否有和temp节点值相同的节点，若存在则temp的fail节点指向该节点，如不存在继续寻找该fail节点的fail节点，直到找到与相同值的节点或达到root节点。

image-20231118121207793

不难发现构建出来的fail指针实际跟KMP算法的next数组类似。

  • 模式匹配

参考：https://blog.csdn.net/bestsort/article/details/82947639

非常形象容易理解

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ALPHABET_SIZE 26    //大小不一定26

// Trie 树节点结构
struct TrieNode {
    struct TrieNode* children[ALPHABET_SIZE];
    struct TrieNode* fail;
    int isEndOfWord;
    int depth;
};

// 队列节点结构
struct QueueNode {
    struct TrieNode* data;
    struct QueueNode* next;
};

// 队列结构
struct Queue {
    struct QueueNode* front;
    struct QueueNode* rear;
};

// 创建新的 Trie 节点
struct TrieNode* createTrieNode() {
    struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
    if (node) {
        for (int i = 0; i < ALPHABET_SIZE; i++) {
            node->children[i] = NULL;
        }
        node->fail = NULL;
        node->isEndOfWord = 0;
        node->depth = 0;
    }
    return node;
}

// 插入字符串到 Trie 树
void insert(struct TrieNode* root, const char* key) {
    struct TrieNode* node = root;
    for (int i = 0; key[i] != '\0'; i++) {
        int index = key[i] - 'a';
        if (node->children[index] == NULL) {
            node->children[index] = createTrieNode();
        }
        node = node->children[index];
        node->depth = i + 1;
    }
    node->isEndOfWord = 1;
}

// 构建AC自动机的失败指针
void buildACAutomaton(struct TrieNode* root) {
    struct Queue queue = {NULL, NULL};
    
    // 将根节点的子节点入队并设置失败指针为根节点
    for (int i = 0; i < ALPHABET_SIZE; i++) {
        if (root->children[i] != NULL) {
            enqueue(&queue, root->children[i]);
            root->children[i]->fail = root;
        }
    }

    while (!isEmpty(&queue)) {
        struct TrieNode* current = dequeue(&queue);

        // 处理当前节点的子节点
        for (int i = 0; i < ALPHABET_SIZE; i++) {
            struct TrieNode* child = current->children[i];
            if (child != NULL) {
                enqueue(&queue, child);

                // 设置失败指针
                struct TrieNode* fail = current->fail;
                while (fail != NULL) {
                    if (fail->children[i] != NULL) {
                        child->fail = fail->children[i];
                        break;
                    }
                    fail = fail->fail;
                }

                if (fail == NULL) {
                    child->fail = root;
                }
            }
        }
    }
}

// 在文本中查找关键词
void findKeywords(struct TrieNode* root, const char* text) {
    struct TrieNode* current = root;
    int charIndex = 0;

    for (int i = 0; text[i] != '\0'; i++) {
        int index = text[i] - 'a';
        while (current->children[index] == NULL && current != root) {
            current = current->fail;
        }
        current = current->children[index];
        if (current == NULL) {
            current = root;
        }
        struct TrieNode* temp = current;
        while (temp != root) {
            if (temp->isEndOfWord) {
                printf("关键词 \"%.*s\" 出现在位置 %d\n", temp->depth, text + charIndex - temp->depth, charIndex - temp->depth);
            }
            temp = temp->fail;
        }
        charIndex++;
    }
}

// 入队操作
void enqueue(struct Queue* queue, struct TrieNode* data) {
    struct QueueNode* newNode = (struct QueueNode*)malloc(sizeof(struct QueueNode));
    if (newNode == NULL) {
        fprintf(stderr, "内存分配失败\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->next = NULL;

    if (isEmpty(queue)) {
        queue->front = newNode;
        queue->rear = newNode;
    } else {
        queue->rear->next = newNode;
        queue->rear = newNode;
    }
}

// 出队操作
struct TrieNode* dequeue(struct Queue* queue) {
    if (isEmpty(queue)) {
        fprintf(stderr, "队列为空\n");
        exit(EXIT_FAILURE);
    }

    struct QueueNode* frontNode = queue->front;
    struct TrieNode* data = frontNode